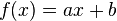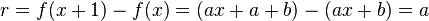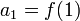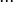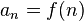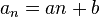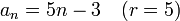Ciąg arytmetyczny

Ciąg arytmetyczny (dawniej postęp arytmetyczny) – ciąg liczbowy, w którym każdy wyraz jest sumą wyrazu bezpośrednio go poprzedzającego oraz ustalonej liczby zwanej różnicą ciągu. Zwykle zakładamy, że wyrazy ciągu arytmetycznego są liczbami rzeczywistymi, choć można rozważać również ciągi arytmetyczne o wyrazachzespolonych.

Definicja formalna i przykłady

Ciąg liczbowy $(a_{n}) \,$ nazywamy ciągiem arytmetycznym, jeśli dla pewnej liczby $r \,$ (nazywanej różnicą ciągu) zachodzi

(\forall n\in\mathbb{N})\ ( a_{n+1}=a_{n}+r)

Równoważnie, $(a_{n}) \,$ jest ciągiem arytmetycznym, jeśli

(\forall n\in\mathbb{N}) \ (\ a_{n+1}-a_n=a_{n+2}-a_{n+1}\ ) \,

Przykłady

ciąg 1, 3, 5, 7, 9, … jest arytmetyczny o różnicy 2,
ciąg 1, 3, 4, 5, 7, 8, 9, 11, 12, … nie jest arytmetyczny (3-1=2 ale 4-3=1),
dowolny ciąg stały jest ciągiem arytmetycznym o różnicy 0.

Własności

Ciąg arytmetyczny o różnicy $r \,$ ma następujący wzór ogólny:

a_n = a_1 + (n-1)r \,

Zatem, aby wyznaczyć pierwszy wyraz $a_1$ ciągu arytmetycznego oraz jego różnicę $r$ wystarczy znać dwa wyrazy tego ciągu.
Trzy liczby ustawione w danej kolejności tworzą ciąg arytmetyczny wtedy i tylko wtedy, gdy środkowa jest średnią arytmetyczną dwóch skrajnych:

a_n = \frac{a_{n-1} + a_{n+1}}{2}

Ciąg arytmetyczny liczb rzeczywistych jest zawsze ciągiem monotonicznym – rosnącym, gdy różnica ciągu jest dodatnia, malejącym, gdy jest ujemna, lub stałym, gdy jest równa 0.

Suma skończonego ciągu arytmetycznego

Suma $S_n$ początkowych n wyrazów ciągu arytmetycznego jest równa średniej arytmetycznej wyrazów pierwszego i n-tego pomnożona przez liczbę wyrazów n:

S_n = a_1+a_2+\dots+a_n=\frac{a_1 + a_n}{2}n =\frac{2a_1 + (n-1)r}{2}n

Formuła zbliżona do powyższej była podana w 1202 przez Leonarda z Pizy w jego dziele Liber abaci (rozdział II.12). Często jest powtarzana historia, według której Carl Friedrich Gauss miał odkryć formułę na sumę ciągu arytmetycznego w wieku siedmiu lat^[1].

Dowód wzoru

Wyraźmy sumę n pierwszych wyrazów ciągu arytmetycznego dwoma sposobami:

S_n=a_1+(a_1+r)+(a_1+2r)+\dots\dots+(a_1+(n-2)r)+(a_1+(n-1)r)

oraz

S_n=(a_1+(n-1)r)+(a_1+(n-2)r)+\dots\dots+(a_1+2r)+(a_1+r)+a_1

(gdzie po prawej stronie drugiego równania sumowane wyrazy ciągu wypisane są w odwrotnej kolejności).

Po dodaniu powyższych dwóch równań stronami otrzymamy

2S_n=\Big(a_1+(a_1+(n-1)r)\Big)+\Big((a_1+r)+(a_1+(n-2)r)\Big)+\dots\dots+\Big((a_1+(n-3)r)+(a_1+2r)\Big)+\Big((a_1+(n-2)r)+(a_1+r)\Big)+\Big((a_1+(n-1)r)+a_1\Big)

a stąd

2S_n=\Big(2a_1+(n-1)r\Big)+\Big(2a_1+(n-1)r\Big)+\dots\dots+\Big(2a_1+(n-1)r\Big)+\Big(2a_1+(n-1)r\Big)+\Big(2a_1+(n-1)r\Big)

2S_n=n(2a_1+(n-1)r)

Pamiętając, że 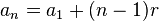$a_n = a_1 + (n-1)r$ , powyższą równość możemy przekształcić do:

S_n=\frac{n[2a_1 + (n-1)r]}{2}=\frac{n( a_1 + a_n)}{2}

Związek ciągu arytmetycznego z funkcją liniową

Istnieje ścisły związek pomiędzy ciągiem arytmetycznym a funkcją liniową y = ax + b. Jeżeli do wzoru funkcji liniowej będziemy podstawiać kolejne wartości argumentówx różniące się o stałą wartość, np. o 1, to otrzymane w ten sposób wartości funkcji liniowej utworzą ciąg arytmetyczny. Jeżeli kolejne argumenty x będą różnić się o 1, to wartości funkcji liniowej będą różnić się o wartość współczynnika kierunkowego a.

Dowód:

f(x)=ax+b

f(x+1)=a(x+1)+b=ax+a+b

r=f(x+1)-f(x)=(ax+a+b)-(ax+b)=a

Jeżeli więc np. założymy, że dziedziną funkcji liniowej będzie zbiór liczb naturalnych dodatnich, to tak otrzymana funkcja będzie ciągiem arytmetycznym o różnicy równej współczynnikowi kierunkowemu prostej (r = a).

Czyli ciąg wartości funkcji liniowej y = ax + b dla kolejnych naturalnych x: