Ciąg
![[1, n]](https://upload.wikimedia.org/math/9/0/d/90d57222b4eae31784ea16305eec5305.png) , lub wszystkim liczbom naturalnym dodatnim, elementów z pewnego ustalonego zbioru[1]. W pierwszym przypadku jest to ciąg skończony, w drugim ciąg nieskończony. Każdej liczbie naturalnej
, lub wszystkim liczbom naturalnym dodatnim, elementów z pewnego ustalonego zbioru[1]. W pierwszym przypadku jest to ciąg skończony, w drugim ciąg nieskończony. Każdej liczbie naturalnej  jest przyporządkowywany tylko jeden element, oznaczany zwykle
jest przyporządkowywany tylko jeden element, oznaczany zwykle  . Elementy
. Elementy 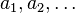 zwane są zwykle wyrazami ciągu. W odróżnieniu od elementów zbioru, kolejność wyrazów ciągu jest istotna, a ta sama wartość może wystąpić w ciągu wielokrotnie.
zwane są zwykle wyrazami ciągu. W odróżnieniu od elementów zbioru, kolejność wyrazów ciągu jest istotna, a ta sama wartość może wystąpić w ciągu wielokrotnie.Definicja i oznaczenia
W szerszym sensie ciąg to dowolna funkcja 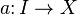 określona na dowolnym zbiorze
określona na dowolnym zbiorze  izomorficznym w sensiestruktury porządkowej z pewnym podzbiorem zbioru liczb naturalnych i o wartościach należących do pewnego zbioru
izomorficznym w sensiestruktury porządkowej z pewnym podzbiorem zbioru liczb naturalnych i o wartościach należących do pewnego zbioru  [2]. Zbiór
[2]. Zbiór  nazywa się zbiorem wskaźników lub indeksów, a jego elementy – wskaźnikami bądź indeksami. Jeśli zbiór wskaźników jest skończony, to sam ciąg również nazywa skończonym, jeśli zbiór
nazywa się zbiorem wskaźników lub indeksów, a jego elementy – wskaźnikami bądź indeksami. Jeśli zbiór wskaźników jest skończony, to sam ciąg również nazywa skończonym, jeśli zbiór  nie jest skończony, to ciąg nazywa się nieskończonym.
nie jest skończony, to ciąg nazywa się nieskończonym.
Wartości funkcji  nazywa się wyrazami bądź elementami ciągu i w miejsce tradycyjnego zapisu
nazywa się wyrazami bądź elementami ciągu i w miejsce tradycyjnego zapisu  stosuje się zwykle zapis
stosuje się zwykle zapis  Sam ciąg oznacza się zazwyczaj nie za pomocą symbolu funkcji, tutaj
Sam ciąg oznacza się zazwyczaj nie za pomocą symbolu funkcji, tutaj  , lecz dłuższej notacji
, lecz dłuższej notacji  lub krótszych jej wariantów
lub krótszych jej wariantów  oraz
oraz  , gdzie napis w nawiasie nazywa się wyrazem ogólnym ciągu. Niekiedy zamiast nawiasów okrągłych stosuje się nawiasy klamrowe, np.
, gdzie napis w nawiasie nazywa się wyrazem ogólnym ciągu. Niekiedy zamiast nawiasów okrągłych stosuje się nawiasy klamrowe, np.  .
.
Zwykle przyjmuje się  (bądź od zera) w przypadku skończonym i pisze często
(bądź od zera) w przypadku skończonym i pisze często  oraz
oraz  w przypadku nieskończonym i zapisuje
w przypadku nieskończonym i zapisuje 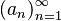 (lub od zera, w zależności od przyjętej definicji liczb naturalnych).
(lub od zera, w zależności od przyjętej definicji liczb naturalnych).
Przykłady
- skończony ciąg pięciu liczb naturalnych:

- nieskończony ciąg stały:

- nieskończony ciąg:

- nieskończony ciąg kolejnych liczb pierwszych:

- nieskończony ciąg następujących liczb wymiernych:

- skończony ciąg dużych liter alfabetu łacińskiego:

Określanie
Wiele ciągów można zdefiniować na kilka równoważnych sposobów, dlatego wybór sposobu zależy zwykle od zastosowań. Należy mieć przy tym świadomość, że liczba tych ciągów, które można opisać za pomocą jednego z poniższych sposobów jest znikoma, choć nieskończona, w porównaniu do wszystkich możliwych ciągów  gdzie
gdzie  są ustalonymi zbiorami nieskończonymi. Wynika to z faktu, iż liczba wszystkich możliwych do zapisania formuł jest co najwyżej przeliczalna, natomiast zbiór wszystkich ciągów jest nieprzeliczalny.
są ustalonymi zbiorami nieskończonymi. Wynika to z faktu, iż liczba wszystkich możliwych do zapisania formuł jest co najwyżej przeliczalna, natomiast zbiór wszystkich ciągów jest nieprzeliczalny.
Podanie wzoru na wyraz ogólny
Jeżeli wyraz ogólny  jest (względnie nieskomplikowaną) funkcją wskaźnika
jest (względnie nieskomplikowaną) funkcją wskaźnika  , np.
, np.
 lub
lub  , czy
, czy  ,
,
to ciąg można określić wskazując ten związek, np.
Wskazanie wyrazów
Jeśli ciąg jest skończony i ma niewiele wyrazów, to najszybszą metodą jest zwykle podanie tych wyrazów (jak to uczyniono w pierwszym przykładzie we wstępie). Jeśli wyrazów jest więcej, to zwykle korzysta się z domyślności czytelnika względem wzoru na wyraz ogólny, z tego powodu reguła wiążąca wskaźnik z wyrazem o tym wskaźniku powinna być w tym wypadku szczególnie prosta, np.
 .
.
Jeżeli wyrazów jest więcej, to wypisanie kilku początkowych i końcowych wyrazów zwykle wystarcza do odgadnięcia postaci ciągu, np.
 .
.
Podobnie w przypadku ciągów nieskończonych, gdzie nie podaje się z oczywistych względów ostatniego wyrazu:
 .
.
Określenia rekurencyjne
Definicja rekurencyjna jest to definicja, w której w wyrażeniu definiującym obok symbolu zmiennej n występuje symbol definiowanego ciągu – jest to więc równanie funkcyjne. W praktyce oznacza to, że wyraz ciągu zależy nie tylko od zmiennej n, ale także jednego lub kilku wyrazów poprzednich.
Przykładem ciągu, w którym każdy wyraz zależy od dwóch poprzednich wyrazów, jest ciąg Fibonacciego dany wzorem
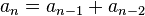 dla
dla 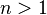 ,
,
przy czym  oraz
oraz  . Oczywiście dany wyraz może zależeć od jednego wyrazu, np. ciąg kolejnych silni można zadać wzorem:
. Oczywiście dany wyraz może zależeć od jednego wyrazu, np. ciąg kolejnych silni można zadać wzorem:
 ,
,
z warunkiem  , jak i od wszystkich poprzednich wyrazów ciągu, np. ciąg liczb Bernoulliego zadaje się równaniem
, jak i od wszystkich poprzednich wyrazów ciągu, np. ciąg liczb Bernoulliego zadaje się równaniem
 dla
dla  ,
,
gdzie 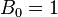 .
.
Ciąg naprzemienny dany wzorem  można zdefiniować rekurencyjnie jako
można zdefiniować rekurencyjnie jako
 dla
dla  ,
,
przymując  Z drugiej strony często pożądana jest definicja jawna (nierekurencyjna) ciągów określonych rekurencyjnie, ma ją np. wyżej wspomniany ciąg liczb Bernoulliego:
Z drugiej strony często pożądana jest definicja jawna (nierekurencyjna) ciągów określonych rekurencyjnie, ma ją np. wyżej wspomniany ciąg liczb Bernoulliego:
 .
.
Do definiowania ciągu niekiedy wykorzystuje się inny wcześniej dany ciąg; przykładami mogą być opisane dalej szeregi, czy iloczyny nieskończone, których wyrazy zależą od poprzedniego i wyrazu o tym samym wskaźniku innego ciągu.
Definicje rekurencyjne są bardziej „eleganckie” od wzoru na wyraz ogólny, lecz cechuje je zwykle duża złożoność obliczeniowa.
Definicje opisowe
Słowny opis wyrazów ciągów jest często łatwiejszy niż wymienione wyżej metody, a bywa jedynym z możliwych. Zawsze jednak, gdy to możliwe, definicję formalizuje się w postaci jednej z powyższych metod. Aby jednak taka metoda była użyteczna w zastosowaniach, musi być wystarczająco prosta. Często wystarczy ograniczyć się dofunkcji elementarnych, jednak najbardziej naturalną klasą funkcji zdają się być funkcje obliczalne, czyli te, dla których istnieje reguła wyliczania jej kolejnych wartości dla kolejnych wskaźników. Niezależnie od tego wykorzystuje się także funkcje rozważane w analizie matematycznej, które umożliwiają w dość zwięzły sposób zdefiniowanie trudnych w innym opisie ciągów, np. funkcja π (pi), która ustala liczbę liczb pierwszych nie większych od danej, definiuje ciąg
 ,
,
czy funkcja ζ (zeta/dzeta), która pozwala równoważnie zdefiniować wyżej opisany ciąg liczb Bernoulliego.
Własności
Ponieważ ciągi definiuje się jako funkcje, to do ich określania stosuje się pojęcia związane z funkcjami, np. ciąg stały, ciąg monotoniczny (rosnący, malejący,niemalejący, nierosnący), czy ciąg ograniczony.
Jeśli struktura określona na zbiorze elementów ciągu umożliwia mówienie o granicy ciągu, np. struktura metryczna, to ciąg, który ma granicę (właściwą) nazywa sięzbieżnym, a w przeciwnym wypadku mówi się, iż jest on rozbieżny. Ciąg spełniający tzw. warunek Cauchy’ego, czyli ciąg, którego wyrazy „zbliżają się” do siebie, nazywa się ciągiem Cauchy’ego.
O ciągach zbiorów można powiedzieć, że są zstępujące lub wstępujące w zależności od tego, czy kolejne wyrazy (zbiory) ciągu zawierają się w poprzedzającym, czy w kolejnym.
Rodzaje
W przypadku, gdy elementy należą do pewnego ciała (np. liczb wymiernych, czy rzeczywistych), można wyróżnić następujące, ważne rodzaje ciągów:
- arytmetyczny z parametrami: różnicą
 oraz wyrazem początkowym
oraz wyrazem początkowym  ,
,
 w postaci rekurencyjnej,
w postaci rekurencyjnej, w postaci jawnej,
w postaci jawnej,
- geometryczny z parametrami: ilorazem
 i wyrazem początkowym
i wyrazem początkowym  ,
,
 w postaci rekurencyjnej,
w postaci rekurencyjnej, w postaci jawnej.
w postaci jawnej.
Szereg definiuje się rekurencyjnie jako ciąg 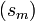 zależny od ciągu
zależny od ciągu  według reguły
według reguły
 ,
,
gdzie  W postaci jawnej zapisuje się go zwykle jako ciąg tzw. sum częściowych,
W postaci jawnej zapisuje się go zwykle jako ciąg tzw. sum częściowych,
 ,
,
co tylko pozornie omija rekurencyjną naturę definicji. Jeżeli  jest ciągiem funkcyjnym, to szereg również nazywa się szeregiem funkcyjnym.
jest ciągiem funkcyjnym, to szereg również nazywa się szeregiem funkcyjnym.
Podobnie definiuje się iloczyny nieskończone jako ciągi  zależne od ciągów
zależne od ciągów  w następujący sposób:
w następujący sposób:
 ,
,
przy czym  .
.
Stosuje się też różne nazwy ciągu stosownie do zbioru jego elementów: w przypadku zbioru liczb mówi się o ciągach liczbowych, bądź bardziej precyzyjnie, np. w przypadku zbioru liczb całkowitych, rzeczywistych czy zespolonych, ciąg nazywa się odpowiednio ciągiem całkowitoliczbowym, rzeczywistym i zespolonym. Jeśli elementami zbioru są funkcje, to ciąg nazywa się ciągiem funkcyjnym. Ciąg powstały poprzez wybranie elementów danego nazywa się podciągiem.
Przestrzenie ciągów
W zbiorze  ciągów
ciągów  o elementach z ustalonego ciała
o elementach z ustalonego ciała  , gdzie
, gdzie  jest pewnym zbiorem wskaźników można określić działania wprowadzając tym samym pewną strukturę algebraiczną, bądź wprowadzić w niej metrykę wprowadzającą strukturę topologiczną.
jest pewnym zbiorem wskaźników można określić działania wprowadzając tym samym pewną strukturę algebraiczną, bądź wprowadzić w niej metrykę wprowadzającą strukturę topologiczną.
Dodawanie
Sumę dwóch ciągów definiuje się zwykle jako ciąg o wyrazach będących sumą odpowiednich wyrazów tych ciągów,
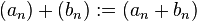 .
.
Wśród ciągów o elementach z ustalonego ciała można wyróżnić ciąg stale równy zeru, który pełni rolę elementu neutralnego dodawania ciągów.
Dla danego ciągu można również wyróżnić element przeciwny, będący ciągiem o wyrazach przeciwnych do danego, czyli
 .
.
Działanie to prowadzi do określenia odejmowania i wprowadzenia struktury grupy (przy czym można je określić na ciągach elementów z uboższej struktury algebraicznej, np. grupy i dalej uogólniać).
Mnożenie
Mnożenie dwóch ciągów,
 ,
,
można określić jako
 ,
,
co czyni z  pierścień (z dzielnikami zera).
pierścień (z dzielnikami zera).
Przyjęcie definicji Cauchy’ego (wariantu splotu dyskretnego, por. mnożenie Cauchy’ego szeregów i macierzy),
 ,
,
przy założeniu, że zbiór wskaźników  zadaje w
zadaje w  strukturę pierścienia bez dzielników zera. Struktura ta jest izomorficzna z sumą prostą
strukturę pierścienia bez dzielników zera. Struktura ta jest izomorficzna z sumą prostą  egzemplarzy
egzemplarzy  . Można w niej zanurzyć pierścień wielomianów o współczynnikach z
. Można w niej zanurzyć pierścień wielomianów o współczynnikach z  .
.
Mnożenie przez skalar
Działanie mnożenia ciągu przez ustalony element z ciała (mnożenie przez skalar),
 ,
,
czyni z  wraz z dodawaniem przestrzeń liniową (jeśli rozpatruje się ciągi o elementach z ciała) lub moduł (jeśli elementy ciągów pochodzą z pierścienia) nad
wraz z dodawaniem przestrzeń liniową (jeśli rozpatruje się ciągi o elementach z ciała) lub moduł (jeśli elementy ciągów pochodzą z pierścienia) nad  . Jeśli
. Jeśli  jest skończony, to
jest skończony, to  z działaniami dodawania ciągów i mnożenia ich przez skalar nazywa się przestrzenią współrzędnych.
z działaniami dodawania ciągów i mnożenia ich przez skalar nazywa się przestrzenią współrzędnych.
Struktura topologiczna
W przestrzeni liniowej ciągów o elementach z ciała  można określić strukturę przestrzeni unormowanej. Klasa norm postaci
można określić strukturę przestrzeni unormowanej. Klasa norm postaci
umożliwia wyróżnienie podprzestrzeni tych ciągów, dla których norma  jest skończona, co czyni z
jest skończona, co czyni z  przestrzeń Banacha.
przestrzeń Banacha.


